El Dibujo
Artículos con consejos y técnicas para el dibujo de la talla en madera.
Lo visto hasta ahora nos ha permitido ver que cultura, arte y ciencia vienen de lejos y de tal forma se complementan que no hay un motivo decorativo considerado artístico por una cultura que no tenga detrás un dibujo lineal con base científica.
También hemos visto que la geometría, (de geos, tierra y metría , medir) como otras áreas matemáticas ya conocidas por los griegos, puede ser muy útil. Nos ha permitido vislumbrar que es posible racionalizar formas de extraña simetría, y relaciones mágicas, divinas o valiosas que la estética humana ha necesitado y seguirá necesitando para desarrollar el arte.
Leer más...
En ese retorno a la cultura griega que caracterizó los siglos XV y XVI los artistas estudiaron intensamente la geometría necesaria para sus dibujos. Quisieron hallar la razón que se escondía detrás de la perfección del arte helénico. Y sin duda lo lograron.
El Laocoonte fue descubierto el 14 de enero de 1506 en las excavaciones de las Termas en el área del palacio del emperador Tito (79-81 d.C.). Su descubrimiento causó un enorme revuelo. El escultor Francesco da Sangallo y Miguel Ángel presenciaron la excavación de la obra y comprendieron el valor artístico de la misma aconsejando al papa Julio II que la adquiriera.
Leer más...
La relación áurea.
¡Agarraros que vienen curvas! …
Dibujemos una línea recta y sobre ella un segmento negro de longitud μ.
Coloquemos delante otro segmento, este de color azul y de longitud menor α.
El segmento mayor que es la suma de ambos lo vamos a llamar ω.
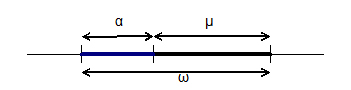
μ (“mu”) es el segmento intermedio que permite al principio α (“alfa”) alcanzar el fín ω (“omega”).
Leer más...
Introducción (III)
Queremos dividir el tiempo Cronos en seis partes o dibujar la rueda de oro del carro de Artemisa, dividir el universo en seis regiones, dibujar un hexágono, o dicho de otra forma más prosaica dividir la circunferencia en 6 partes iguales.
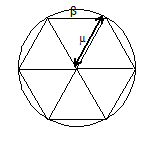
¿Qué valor tiene µ en nuestro dibujo? No hace falta ser un matemático famoso para ver que es el mismo que el radio. Y efectivamente los triángulos son equiláteros, de forma que el lado del hexágono β también mide el radio del compás con el que hemos dibujado la circunferencia. ¡Me seguís, o voy muy rápido…!
Con el hexágono podemos construir una estrella de seis puntas.
Leer más...
Introducción (parte I de V).
Aunque podríamos remontarnos más atrás en el tiempo, bastará con hacer un breve viaje 
a la Grecia clásica.
Desde el siglo IX antes de cristo los griegos eligieron un grupo de caracteres de dibujo lineal para crear un “alfabeto”, αλφάβητο (palabra de origen griego que deriva de αβ).
Ánfora griega del llamado
periodo geométrico inicial,
año 1000 a 900 a.c .
Leer más...
