Introducción (III)
Queremos dividir el tiempo Cronos en seis partes o dibujar la rueda de oro del carro de Artemisa, dividir el universo en seis regiones, dibujar un hexágono, o dicho de otra forma más prosaica dividir la circunferencia en 6 partes iguales.
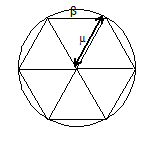
¿Qué valor tiene µ en nuestro dibujo? No hace falta ser un matemático famoso para ver que es el mismo que el radio. Y efectivamente los triángulos son equiláteros, de forma que el lado del hexágono β también mide el radio del compás con el que hemos dibujado la circunferencia. ¡Me seguís, o voy muy rápido…!
Con el hexágono podemos construir una estrella de seis puntas.
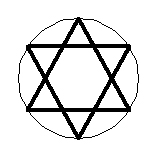Es difícil permanecer indiferentes al recuerdo del genocidio de 6 millones de personas que en 1941 fueron señalados con esta figura. Cada esquina representa 1 millón de personas. Si sumas las cifras de la fecha 1941 se obtiene la cifra 15 que sumada y reducida a una cifra también da 6.¡La magia nos rodea, sólo hay que querer encontrarla!
Ahora queremos viajar 2 mil años atrás en el tiempo y dibujar el símbolo que identifica a una escuela de pensadores griegos cuyo lema es “todo es número”. ¡Esperemos que no!. Algunos seguimos con la esperanza de que no sea así, pero la ciencia nos lo pone difícil.
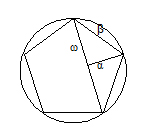
Πυθαγόρας o Pitágoras (582 a 507 a.c) y sus seguidores doscientos años antes que Euclides ya sentían un interés especial por el pentágono y no sólo por lo difícil que resulta dividir la circunferencia en 5 partes iguales con compás y regla, que ya manejaban con soltura.
Descubrieron que había un número φ que parecía intrínseco de este polígono. ¿Cómo?... pues buscando la magia del pentágono (πεντάγωνο).
Al dividir la diagonal del pentágono entre su lado se obtenía un número enigmático.
Pero no sólo eso, si se dividía el lado entre el valor de la bisectriz se volvía a obtener la misma relación. 
Pero queríamos dibujarlo. En este caso μ es el radio pero parece que β es un poco mayor que μ.
Ocurre que si dividimos el valor del radio por φ y llevamos ese valor a la separación de las patas de un compás logramos dividir la circunferencia en 10 partes iguales que nos permiten dibujar nuestro pentágono.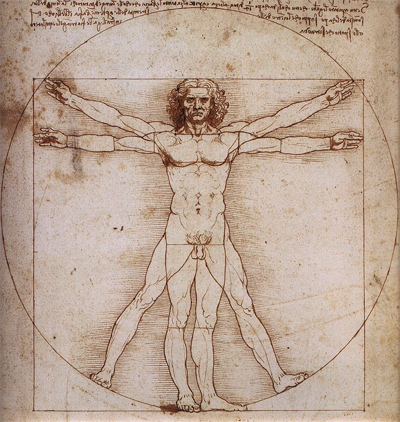 
No es esta la única manera de dibujar un pentágono o un decágono.
Tened por seguro que en este terreno, los pintores, escultores y arquitectos del renacimiento podrían darnos lecciones.
No podemos hacer una introducción al dibujo sin hablar del “ars renascens”.
Lo veremos en la siguiente entrega.
